Quantum Mechanics

Here we discuss the meaning of a partial trace and show how to perform this operation. We provide explicit examples and a python implementation that is intended to be instructive, but is not (at all) optimized for efficiency.

We first consider the canonical example of two coupled two-level systems, sites a and b.

The basis states of this system are $\ket{00}$ , $\ket{01}$ , $\ket{10}$ , $\ket{11}$ , for $\ket{q_a, q_b}$ and the density matrix is:

$\rho =\begin{bmatrix} \rho_{00,00} & \rho_{00,01} & \rho_{00,10} & \rho_{00,11} \\ \rho_{01,00} & \rho_{01,01} & \rho_{01,10} & \rho_{01,11} \\ \rho_{10,00} & \rho_{10,01} & \rho_{10,10} & \rho_{10,11} \\ \rho_{11,00} & \rho_{11,01} & \rho_{11,10} & \rho_{11,11} \\ \end{bmatrix}$

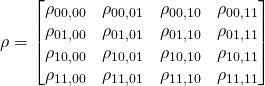
The reduced density matrix for one of these sites can be computed by the partial trace. For site a the reduced density matrix is:

\rho_{a} = \begin{bmatrix}

\rho_{00, 00} + \rho_{01,01} & \rho{10,10} + \rho{11